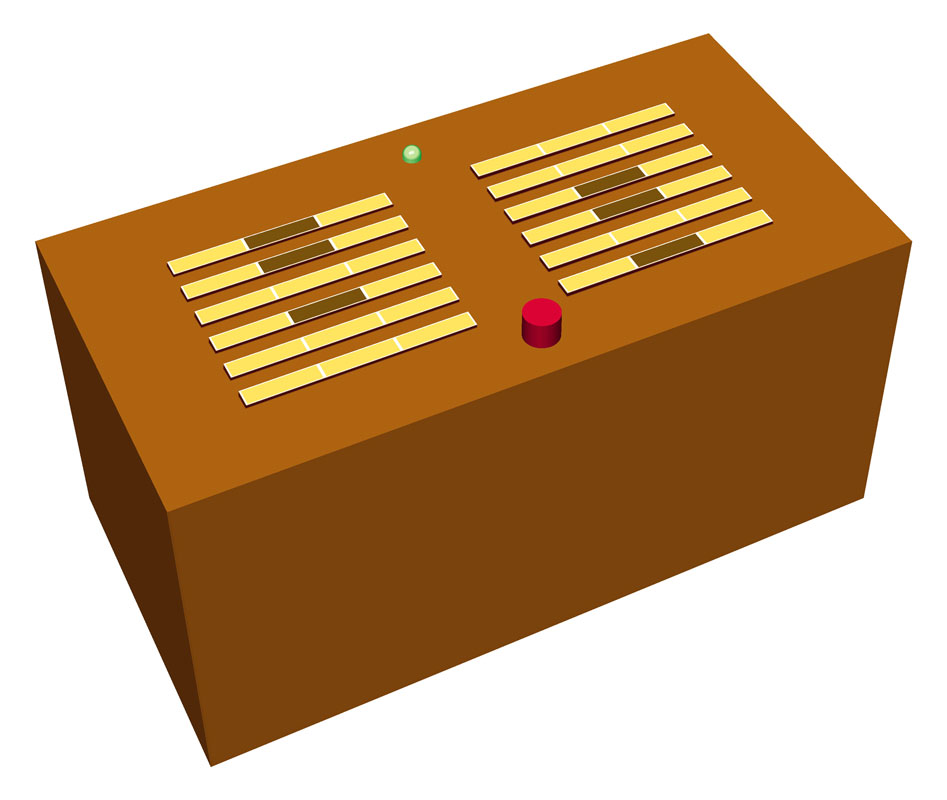
In my previous column I described an electronic version of that old fortune-telling favorite, the Magic 8 Ball (Make: Volume 30, “Magic 8 Box”). Now I want to delve deeper into divination — and the deepest you can go is surely the I Ching. This tool of prophesy originated in China thousands of years ago.
The I Ching supposedly offers insight into your current situation, and how it may change in the near future. You use a random system to draw 2 “hexagrams,” each of which consists of 6 lines that can be solid or broken in the middle. (A solid line represents yang energy, while a broken one is yin, in case you were wondering.) The left hexagram interprets your current situation. Some believe the right one suggests your future (seen below).

To find out what the hexagrams mean, you look them up in a book. Dozens are available, but the one I use is The I Ching: The Book of Answers by Wu Wei, because its interpretations are dumbed down to a level where people such as myself, who are philosophically impaired, can make sense out of them.
You draw the hexagrams from the bottom up, by tossing coins — or by “casting yarrow stalks,” if you’re a traditionalist. (Yarrow is a weed, and you can find suppliers of dried stalks online.) Mathematically speaking, there are 4 possible present/future combinations for each pair of lines, as shown in the chart below.

Now, here’s the catch. The combination probabilities in the chart are what you get when you perform complex operations with yarrow stalks. Using coins will alter this pattern, giving every combination an equal probability. I wanted my electronic I Ching to be as authentic as possible, so I stuck with the ancient, yarrow-stalk probability set, even though this made the circuit a bit more complicated.
To display the hexagrams, I used light bars — little rectangles containing LEDs. Each line in a hexagram can be represented by 3 bars placed in a row, with the end bars lit and the center bar switched on to represent a solid line, or off to represent a broken line.
This article first appeared in Make: Vol. 31, page 158.