Topology Tuesday: Klein’s Quartic

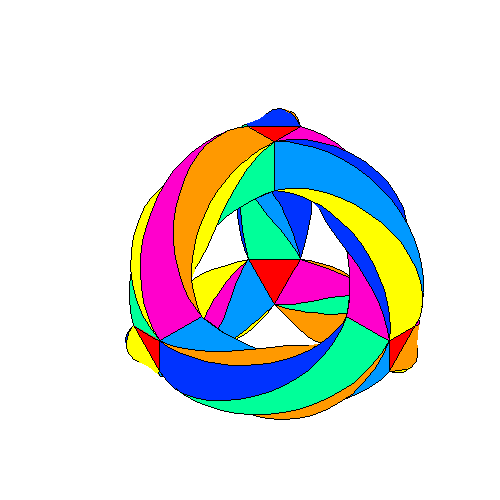
If you are looking for a subject likely to inflame the hearts of mathematicians, make them slightly weak in the knees, and induce some distinctly poetical sentiments, Klein’s Quartic, first described by German mathematician Felix Klein in 1878, seems like a pretty good bet. Though the surface itself, per Wikipedia, “does not have a (non-trivial) 3-dimensional linear representation,” several prominent math-bloggers have produced models, projections, and plain-language written explanations attempting—and doing a pretty good job of it, IMHO—to communicate their passion for the construct:

• Sci-fi author Greg Egan is also the author of the striking animation that leads this post. It depicts an unusual symmetry operation upon an “embedding” of Klein’s Quartic in 3-dimensional space.
• UC-Riverside Professor John Baez’s page provides a longer and more in-depth, but still novice-accessible, explanation of just what the heck Klein’s quartic is, mathematically. It also includes some alternative embeddings and projections of the surface that are quite lovely.
• Edmund Harriss of Maxwell’s Demon, who put me onto this Klein Quartic business in the first place, steps us through the construction of a partial model of the quartic using spherical magnets.
• UC-Berkeley’s Mathematical Sciences Research Institute has published a free anthology of papers on the quartic titled The Eightfold Way: The Beauty of Klein’s Quartic Curve.

The Eightfold Way is also the title of a sculpture derived from Klein’s Quartic that resides on the MSRI campus in Berkeley. [Thanks, Edmund!]