Take me to the Steps

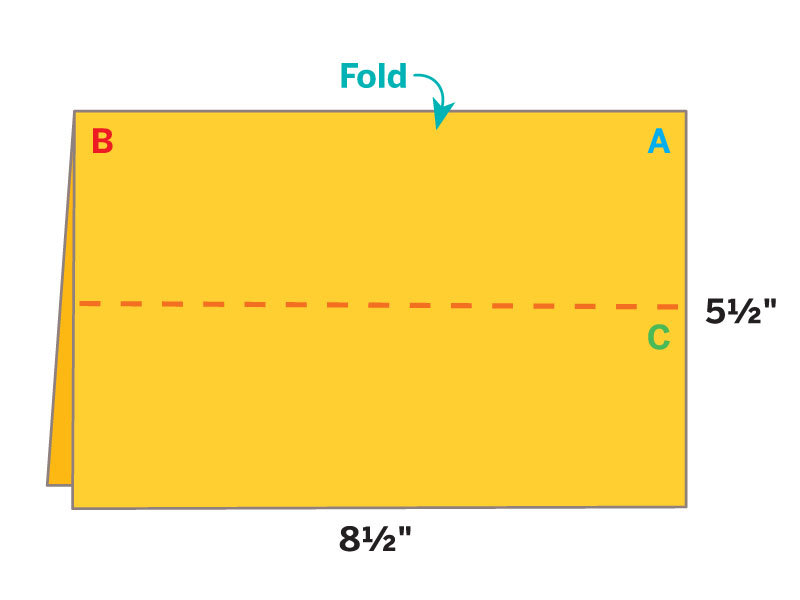
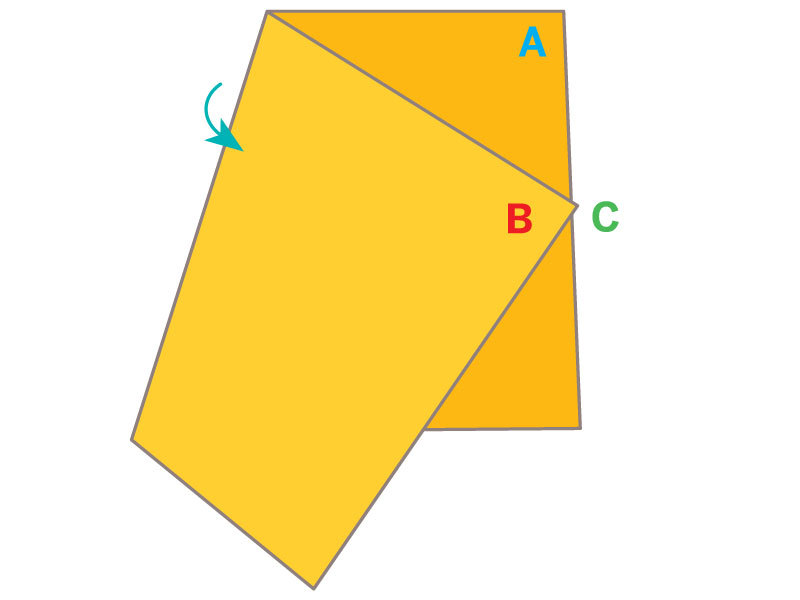
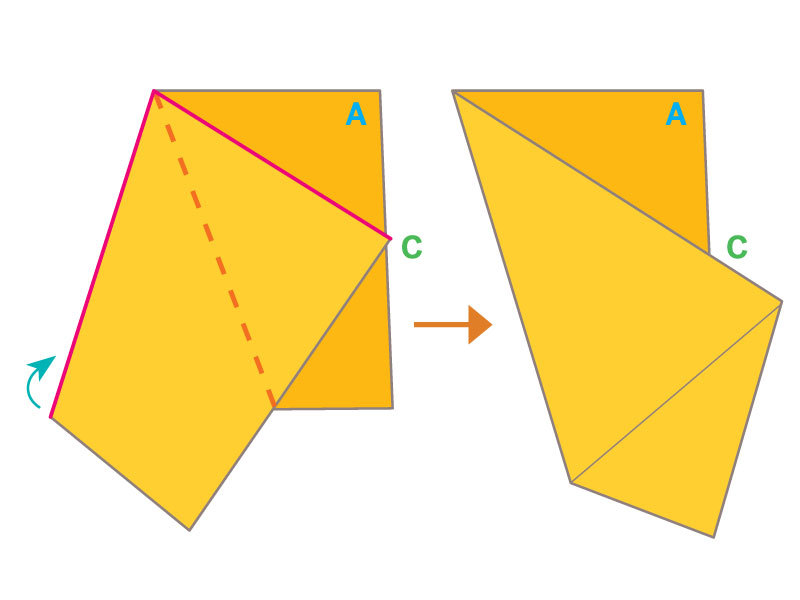
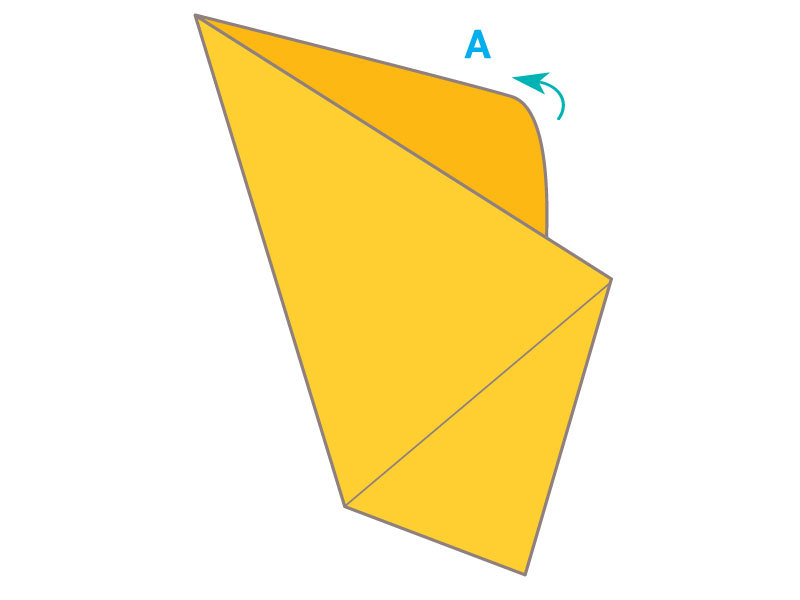
Historical legend tells us that seamstress Betsy Ross was visited in 1776 by George Washington, Robert Morris, and George Ross, who asked her to make an American flag conforming to a resolution of the Continental Congress.

Washington’s design had 13 alternating stripes of white and red, and 13 six-pointed stars on a field of blue. Betsy suggested five-pointed stars instead. When someone wondered whether five-pointed stars would be more difficult to make, Betsy showed how fabric could be cleverly folded to allow a five-pointed star to be made with just one cut of the scissors.

It’s a pretty story, but like many fables of our early history, it’s probably a myth. Contemporary documentation of it is totally lacking. Betsy’s grandson first related the story in 1870, nearly a century after the fact, admitting that he had no confirmation other than stories passed down in the family.

The story quickly proliferated, being published in Harper’s New Monthly Magazine in 1873, finding its way into other publications and even into textbooks, persisting even now. And the Betsy Ross House in Philadelphia is the second-most-visited historic site there, but there’s no hard evidence that she ever lived in it.

We’ll leave historians to sort all that out. You can find out more about the flag myth. What catches my interest is the method of folding cloth to obtain a five-pointed star with a single scissors cut. It’s the one believable detail in this story. Creating five-fold symmetric figures is a challenge in Euclidean geometry, and with paper folding, too. But a method is well known to quilters and seamstresses and was surely known to flag makers of colonial times and earlier.

What will the next generation of Make: look like? We’re inviting you to shape the future by investing in Make:. By becoming an investor, you help decide what’s next. The future of Make: is in your hands. Learn More.

Project Steps

Construct the star.

Here are the instructions to make a star template using a sheet of thin 8½”×11″ paper:

Fold the paper in half, to 8½”×5½”, with the fold at the top. Then fold the paper in half again to make a temporary crease to locate point C at the midpoint of the right edge. This crease is shown as a dotted line.

Mark the upper right corner “A” so you won’t lose track of it. Mark the upper left corner “B.”

Bring corner B over to point C, just at the midpoint of the right edge of the paper, on the crease you made earlier. The left portion of the top edge of the paper folds over, making an angle along the solid line to point C. This angle is the foundation of the construction.

The angle is approximately 35.85584°. This is smaller than 36°— one tenth of a full circle — but very close to what we need to define the polygon vertices that are the basis of a five-pointed star.

This is an approximate construction, not a strictly Euclidean construction. (Euclidian constructions don’t use measuring tools. This construction starts with a measured rectangle of paper.)

Fold the lower left edge up to lie along the slanted fold that passes through point C.

Grabbing hold of point A, fold the paper backward along the diagonal so that all edges coincide. This will make an angle of approximately 36°.

Now turn the whole thing over. Notice that there’s a right triangle on the top of the folded stack of paper.

Draw a line — starting about 1/3 of the way in along the long (top) side — to the lower corner of the triangle.

Use suitably heavy scissors to cut the whole stack along the line and unfold the paper.

You should now have a near-perfect five-pointed star like the one shown in the photo. Other variations can be obtained by tilting the cut line differently. Cut from the lower corner to the midpoint of the opposite side and you get a “fat” star. Experiment for other variations. The remainder of the sheet of paper can be used as a stencil to decorate your house or automobile with painted stars.

Conclusion

Afterthoughts

You may wonder whether 8½"×11" paper was common in 1776. If it wasn’t, this would suggest that the Betsy Ross flag story is a fabrication. (I coudn’t resist that one.) But yes, 8½"×11" paper was available then. That size goes back to Europe in 1600, the result of a 17"×22" sheet cut into four pieces. Not until the time of the first World War did 8½"×11" paper become standard for business in the United States. I’ve tried similar constructions starting with sheets of other sizes, but these usually result in awkward unanticipated difficulties.

The story of the invention of this star construction method remains to be told. Who was the clever person who discovered it? I shall resist idle speculation about how the size of paper necessary for this construction might mystically relate to the Golden Mean or to the Fibonacci sequence.

Congress did not specify how the stars were to be arranged. Many flags of that time and earlier had “stars and stripes,” with the stars arranged in various ways. Flags with stars in a circle were rare. A painting by Charles H. Weisgerber, made in 1870, shows Betsy Ross stitching a flag with stars in a circle while Washington, Morris, and George Ross look on.

That suggests another mystery. What trick of geometry, or origami, would you need in order to arrange 13 stars perfectly spaced around a circle?

This project frist appeared in MAKE Volume 19, page164.